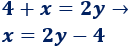Métodos de solución de sistemas de dos ecuaciones lineales con dos incógnitas
Suma y resta (Reducción o eliminación)
Igualación
Sustitución
Crammer
La regla de Cramer sirve para resolver sistemas de ecuaciones lineales. Se aplica a sistemas que cumplan las dos condiciones siguientes:
El número de ecuaciones es igual al número de incógnitas.
El determinante de la matriz de los coeficientes es distinto de cero.
Tales sistemas se denominan sistemas de Cramer.
Sea Δ el determinante de la matriz de coeficientes.
Y sean:Δ 1, Δ 2 , Δ 3 ... , Δ n
Los determinantes que se obtiene al sustituir los coeficientes del 2º miembro (los términos independientes) en la 1ª columna , en la 2ª columna, en la 3ª columna y en la enésima columna respectivamente.Un sistema de Cramer tiene una sola solución que viene dada por las siguientes expresiones:
El método de eliminación consiste en realizar la sumatoria de ambas ecuación con la finalidad de que alguna de las incógnitas desaparezca en el resultado de dicha operación.Por lo general, es necesario realizar una serie de pasos pertinentes para que ambas ecuaciones lo permitan.
Paso 1. Se preparan las ecuaciones multiplicándolas por los números que convenga.
Para ello elegimos arbitrariamente cuál incógnita queremos eliminar; en este caso optamos por eliminar a la variable x.
La variable x viene representada por un 2x. Esto implica que para eliminarla al sumar dicha ecuación con la Ecuación 2, esta última debería tener un -2x con el cual cancelarse o eliminarse.
Por lo tanto es pertinente multiplicar la Ecuación 2 por un factor de -2 de la siguiente manera:
Paso 2. Sumamos ambas ecuaciones.
Paso 3. Se resuelve la ecuación resultante.
Paso 4. El valor obtenido se reemplaza en cualquiera de las ecuaciones iniciales y se resuelve.
En este caso elegimos reemplazar en la Ecuación 2
El método de sustitución consiste en aislar en una ecuación una de las dos incógnitas para sustituirla en la otra ecuación.
- Sustituimos la incógnita en la otra ecuación. Como tenemos que la incógnita x es igual 2y-4, escribimos 2y-4 en lugar de la x en la segunda ecuación (sustituimos la x):
- Resolvemos la ecuación de primer grado obtenida:
- Calculamos la otra incógnita sustituyendo. Al despejar la incógnita x teníamos
Como conocemos y=3, sustituimos en la ecuación:

Por tanto, la otra incógnita es x=2.
La solución del sistema es
El método de igualación consiste en aislar una incógnita en las dos ecuaciones para igualarlas.
Este método es aconsejable cuando una misma incógnita es fácil de aislar en ambas ecuaciones.
- Aislamos una incógnita en las dos ecuaciones. Escogemos aislar la incógnita x:

- Igualamos las expresiones. Como x = x, podemos igualar las expresiones obtenidas:

- Resolvemos la ecuación de primer grado obtenida:

- Calculamos la otra incógnita sustituyendo. Sustituimos el valor de la incógnita y en alguna de las expresiones calculadas anteriormente (la primera, por ejemplo):

La solución del sistema es