Please enable JavaScript.
Coggle requires JavaScript to display documents.
Lógica proposicional y operaciones lógicas (Yulieth garcia) - Coggle…
Lógica proposicional y operaciones lógicas (Yulieth garcia)
¿Qué es la lógica?
La lógica matemática es la disciplina que trata de métodos de razonamiento. En un nivel elemental, la lógica proporciona reglas y técnicas para determinar si es o no valido un argumento dado.
• rama de las matemáticas
– instrumento para representar el lenguaje
natural
– proporciona un mecanismo de deducción
¿Qué son las proposiciones?
Proposición o enunciado: es toda afirmación u oración declarativa que expresa algo sobre lo que se pueda decir si es verdadero o falso.
A continuación se tienen algunos ejemplos de proposiciones válidas y no válidas, y se explica el porqué algunos enunciados no son proposiciones. Las proposiciones se indican por medio de una letra minúscula, dos puntos y la proposición propiamente dicha. Ejemplo.
p: La tierra es plana.
q: -17 + 38 = 21
r: x > y-9
s: El Morelia será campeón en la presente temporada de Fut-Bol.
t: Hola ¿como estas?
w: Lava el coche por favor.
¿Clases de proposiciones?
Proposiciones Simples o atómicas: Son aquellas proposiciones que no se pueden dividir.
EJEMPLO:
El cielo es azul. (verdadero) Nomenclatura: p
Proposiciones Compuestas:
Proposiciones Compuestas.- También denominadas moleculares. Son aquellas que están formadas por dos o más proposiciones simples unidas por los operadores lógicos.
EJEMPLO:
Los lectores de este libro son jóvenes o universitarios.
Si el miércoles próximo me saco la lotería entonces te regalaré un auto.
Fui al banco, pero el banco estaba cerrado.
Se clasifican en dos métodos de razonamiento:
Cálculo
proposicional
Sentencias que expresan relaciones entre
atributos y cualidades de los objetos
Cálculo de
predicados
Establecen propiedades de individuos y
relaciones entre estos
EJEMPLO:
"si el dato es de entrada o de salida y el dato no es de entrada,
entonces es de salida"
p = el dato es de salida
q = el dato es de entrada
{p V q , ¬ p} → q
¿Cuáles son los conectivos que se utilizan en la construcción de las proposiciones?, incluya un ejemplo de su autoría de cada conectivo.
¿Clases de proposiciones?
https://lagusanita.jimdofree.com/conceptos-matem%C3%A1ticos/proposiciones/
∨ Disyunción (“o” inclusivo)
Esta es falsa si las dos proposiciones simples son falsas. "La actividad de clase es resolver ejercicios o realiza la evaluación".
→ Implicación o condicional
Es una proposición compuesta formada por dos proposiciones (p q) unidas mediante el conector → "entonces". La notaremos p → q.
∧ Conjunción
Esta es verdadera si las dos proposiciones simples son verdaderas. "El carro prende si tiene gasolina y electricidad".
↔ Doble implicación o bicondicional
La proposición bicondicional es una proposición compuesta formada por dos proposiciones simples (p q) unidas mediante el conector lógico ↔ "si y sólo si". La notaremos p ↔ q.
¬ Negación
EJEMPLO:
p: Bogotá está a 2.600 metros sobre el el nivel mar. (verdadero)
~ p: Bogotá no está a 2.600 metros sobre el nivel del mar
¿Cómo se construyen las proposiciones?
A través conectores u operadores lógicas que permiten formar proposiciones compuestas (formadas por varias proposiciones). los operadores son los que permiten construir proposiciones compuestas a través de proposiciones simples.
Ejemplo de proposición:
Si la luna está llena y no llueve, entonces saldré
caminar
El curso de Matemáticas Discretas está fácil.
El Último Teorema de Fermat es cierto
Ejemplos: No son proposiciones:
Si la frase es cierta, lo que en ella se dice debe ser cierto, así debe ser falsa.
x + 3 es un número impar
¿Creación de tablas, tautología, contradicción y contingencia?
https://superinteresante7.wordpress.com/2011/10/16/tautologias-contradiccion-y-contingencia/
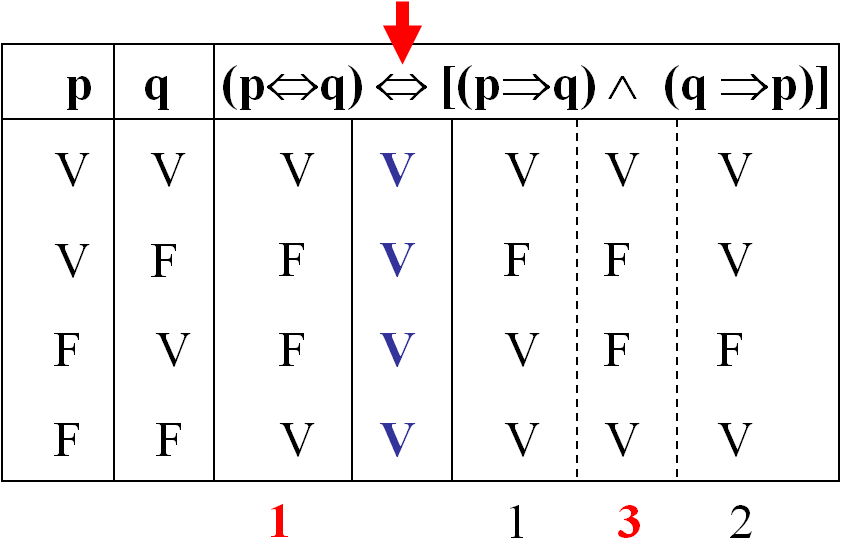
Tautología:
Es una expresión lógica que resulta verdadera para cualquier interpretación; es decir, para cualquier asignación de valores de verdad.
EJEMPLO:
Contradicción.
Una proposición es una contradicción, si es falsa para todos sus valores de verdad .
EJEMPLO:
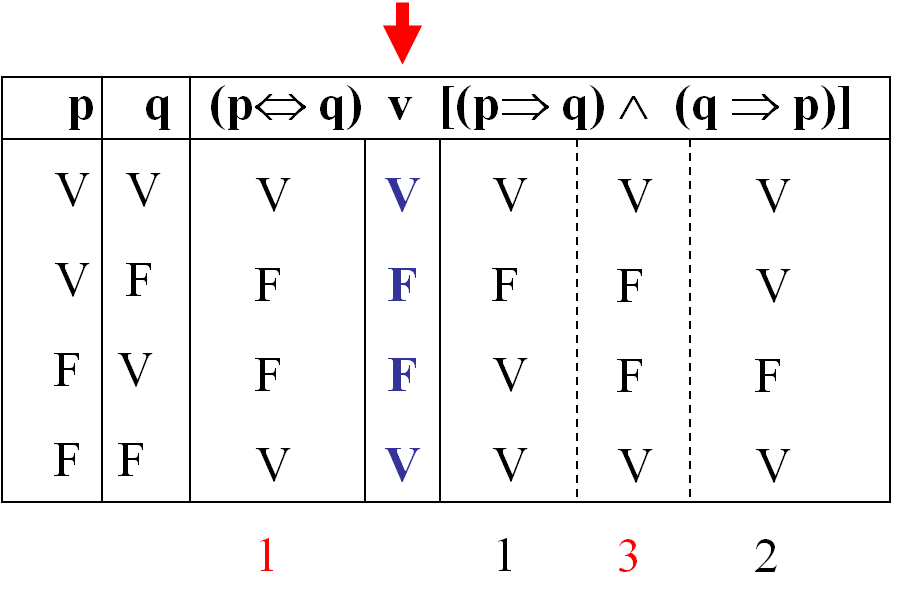
Contingencia:
Una proposición es una contingencia si no es ni verdadera ni falsa independientemente de los valores de verdad de las proposiciones simples que la componen.
EJEMPLO:
Conectivos lógicos:
Es una partícula que se utiliza para formar las proposiciones compuestas, es decir, es un elemento de lenguaje que permite construir proposiciones nuevas a partir de las existentes, obteniendo así nuevos significados.
https://ccc.inaoep.mx/~villasen/CursoMatDiscretas/Logica.pdf
