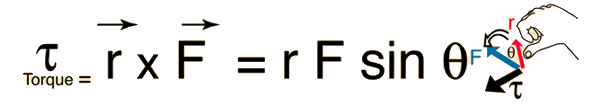DYNAMICS OF ROTATIONAL MOTION
10.1 Angular Momentum - Objects Rotating About a Fixed Axis
-angular momentum, L = Iω
-vector quantity (unit: kgm²/s)
-rotational analogue of the linear momentum, p=mv
Newton's Second Law :
Example :
a) L = I↑ω↓
b)L = I↓ω↑
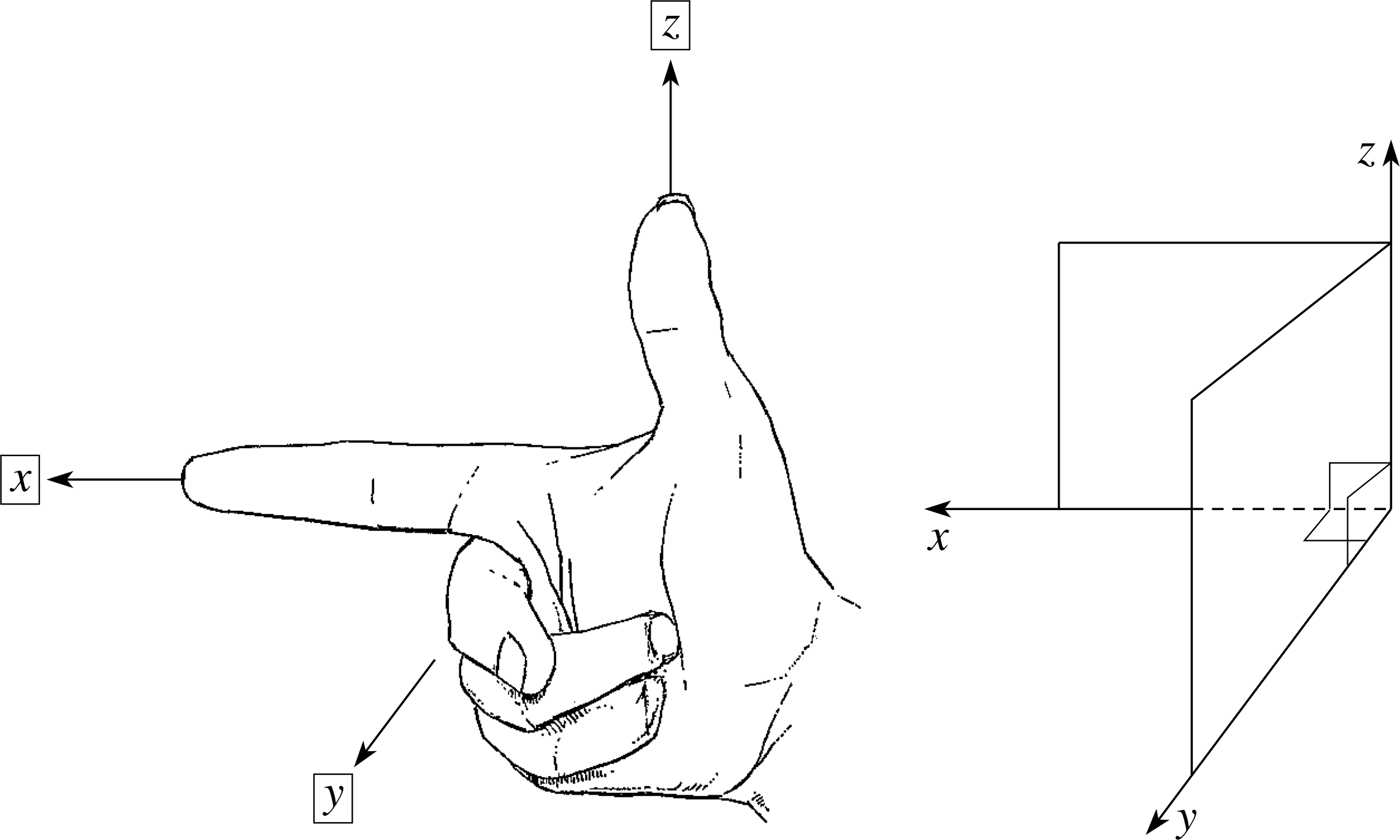
10.2 Vector Cross Product; Torque as a Vector
Using Right-hand rule
written in determinant form :
right hand grib rule
fleming right hand rule
Defination :torque- product of force and the vector from point of action of the force to the axis of rotation
10.4 Angular Momentum and Torque for a System Of Particles; General Motion
10.6 Conservation of Angular Momentum
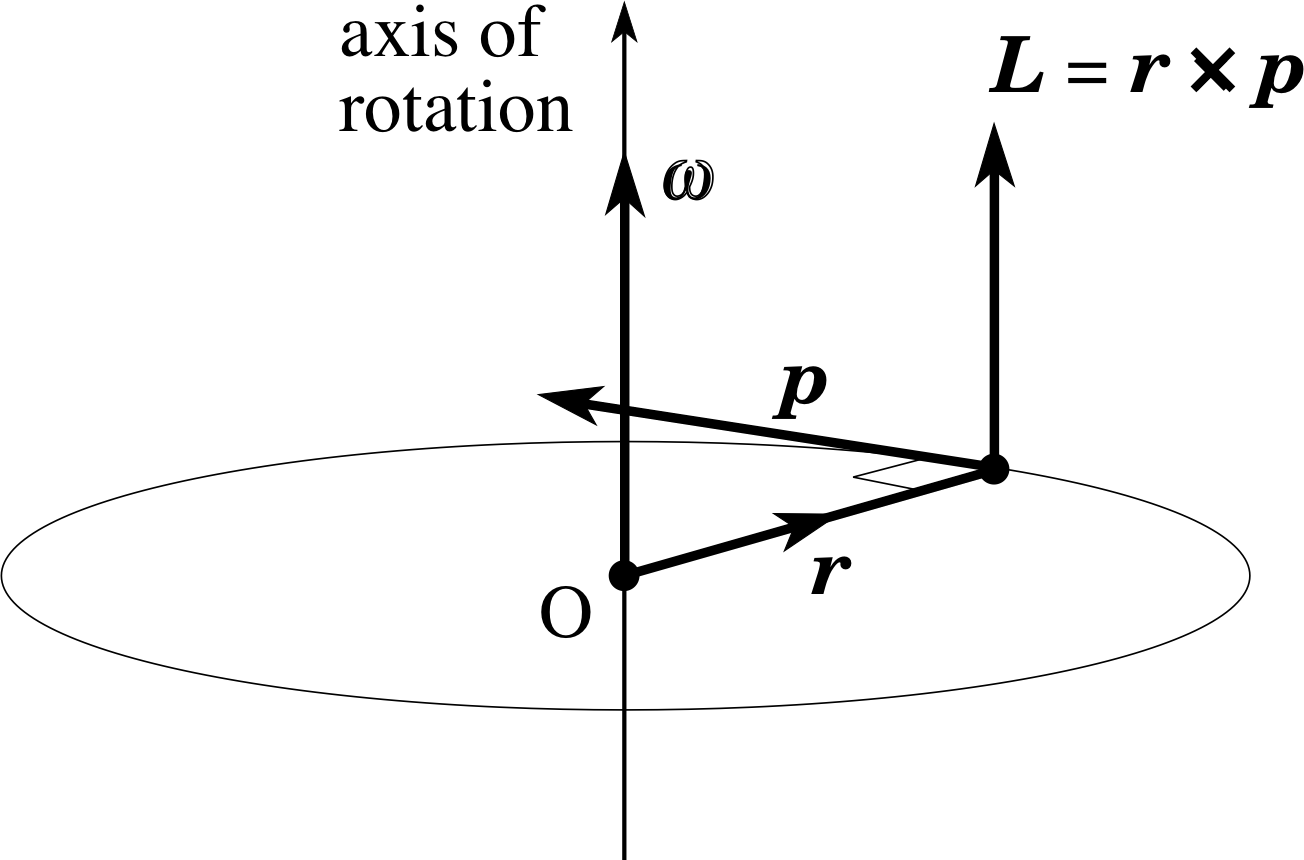
10.3 Angular Momentum of a Particle
9.5 Angular Momentum and Torque for a Rigid Object
L = r x p , where p=mv
Derivation of L :
Relate to Newton's Second Law
angular momentum can change when there is an external torque
Relationship between angular momentum and torque
valid for : origin of an inertial
reference frame & center of mass
For a rigid body , angular momentum L= Iω
System (rotational imbalanced)
the angular momentum and angular velocity in different direction
require vector to keep unbalancing system rotating
total angular momentum of a system remain constant if the net external torque acting on the system is zero
Example :
WONG SIEW HAN A20SC0425
Angular momentum of particle :