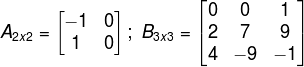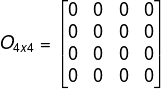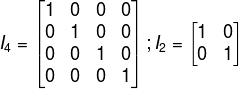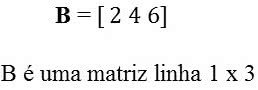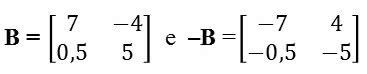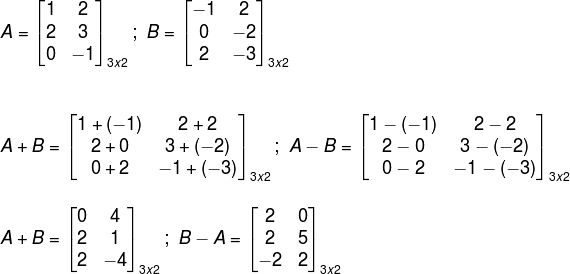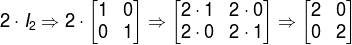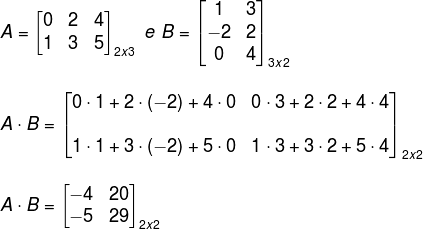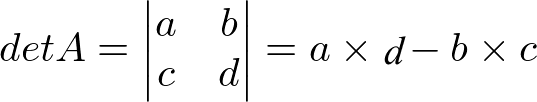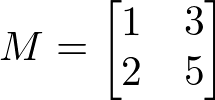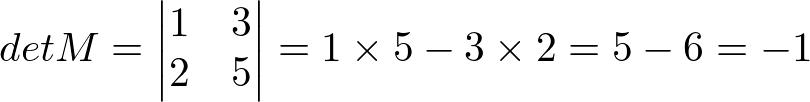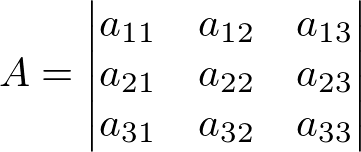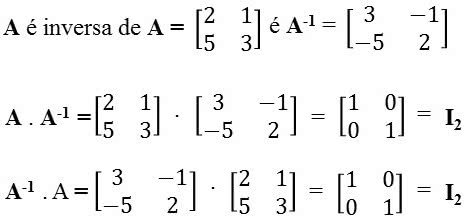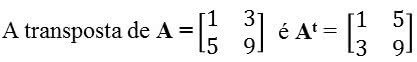Please enable JavaScript.
Coggle requires JavaScript to display documents.
Matriz, dropped image link, dropped image link, dropped image link,…
Matriz
Tipos de matrizes
-
Matriz inversa : Uma matriz quadrada B é inversa da matriz quadrada A quando a multiplicação das duas matrizes resulta em uma matriz identidade In, ou seja, texto A . B = B . A = In fim do texto com texto n fim do texto subscrito fim do subscrito.
-
Matriz Oposta: Na matriz oposta, os elementos entre duas matrizes apresentam sinais diferentes.
-
Igualdade de Matrizes: Quando temos matrizes iguais, os elementos das linhas e das colunas são correspondentes:
-
-
Matriz identidade : Os elementos da diagonal principal são iguais a 1 e os demais elementos são iguais a zero.
Operações entre Matrizes
-
-
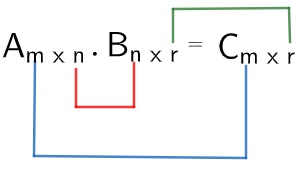
Multiplicação de matrizes:A multiplicação de matrizes não é tão trivial quanto a adição e subtração delas. Antes de realizar a multiplicação, uma condição deve também ser satisfeita em relação à ordem das matrizes. Considere as matrizes Amxn e Bnxr.
-
Para realizar a multiplicação, o número de colunas da primeira matriz deve ser igual ao número de linhas da segunda. A matriz produto (que vem da multiplicação) possui ordem dada pela quantidade de linhas da primeira e quantidade de colunas da segunda.
Para efetuar a multiplicação entre as matrizes A e B, devemos multiplicar cada uma das linhas por todas as colunas da seguinte maneira: o primeiro elemento de A é multiplicado pelo primeiro elemento de B e, em seguida, somado ao segundo elemento de A e multiplicado pelo segundo elemento de B, e assim sucessivamente.
-
-
-
Multiplicação de um número real por matriz: A multiplicação de um número real de uma matriz (também conhecida como multiplicação de matriz) por uma escalar é dada multiplicando cada elemento da matriz pela escalar.
Seja A = [aij]mxn uma matriz e t um número real, então: t · A = [t · aij]mxn
-
Matrizes e determinantes
Um número real recebe o nome de determinante quando está associado a uma matriz quadrada. Uma matriz quadrada pode ser representada por Am x n, onde m = n.
Determinante de matrizes de ordem 1: O determinate de uma matriz de ordem 1×1 é o próprio elemento da matriz.
-
Determinante de matriz de ordem 2
O determinante das matrizes quadradas – aquelas que possuem os mesmo números de linhas e colunas – de ordem 2×2 é calculado pela multiplicação dos elementos da diagonal principal e secundária. Assim:
-
Determinantes de matriz de ordem 3
Para calcularmos o determinante de uma matriz quadrada de ordem 3×3 temos que utilizar a regra de Sarrus.
-
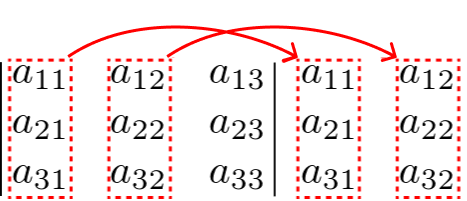
A regra de Sarrus funciona da seguinte maneira: Copiamos a 1ª e 2ª coluna da matriz A para o lado direito da matriz.
-
Depois fazemos o produto entre os termos da matriz com as colunas que copiamos para o lado direito, seguindo as setas abaixo: para as setas azuis, multiplicamos os 3 elementos diagonalmente e associamos os sinais de mais (+); para as setas vermelhas, multiplicamos os 3 elementos de cada seta e associamos o sinal de menos (-).
Então: det A = a11 . a22 . a33 + a12 . a23 . a31 + a13 . a21 . a32 – a13 . a22 . a31 – a11 . a23 . a32 – a12 . a21. a33
Quando a ordem de uma matriz quadrada é superior a 3, geralmente, utiliza-se o Teorema de Laplace para calcular o determinante
Teorema de Laplace
Com o teorema de Laplace podemos encontrar o determinante de uma matriz quadrada A da seguinte forma:
1.Devemos escolher um linha ou coluna aleatoriamente;
2.Somar os produtos dos elementos da linha ou coluna que escolhemos pelos seus cofatores;
3.O determinante de A é o resultado encontrado no item 2.
Matriz é uma tabela organizada em linhas e colunas no formato m x n, onde m representa o número de linhas (horizontal) e n o número de colunas (vertical).
A função das matrizes é relacionar dados numéricos. Por isso, o conceito de matriz não é só importante na Matemática, mas também em outras áreas já que as matrizes têm diversas aplicações.
Na representação de uma matriz, os números reais geralmente são elementos inseridos entre colchetes, parênteses ou barras.
Produto Janeiro /Fevereiro
Bolo de chocolate 500 / 450 Bolo de morango 450 / 490
Essa tabela apresenta dados em duas linhas (tipos de bolo) e duas colunas (meses do ano) e, por isso, trata-se de uma matriz 2 x 2. Veja a representação a seguir:
-
Elementos de uma matriz
As matrizes organizam os elementos de maneira lógica para facilitar a consulta das informações.
Uma matriz qualquer, representada por m x n, é composta por elementos aij, em que i representa o número da linha e j o número da coluna que localizam o valor.
Exemplo: Elementos da matriz de venda da confeitaria.
-
-
-
-
-
-
-
-
-
-
